SPOJ- PIE solution

Hello!

This post is about solution of SPOJ problem PIE :  visit question PIE

So, we will be looking at the implementation part of it using Binary Search.

We encourage you to try solving problem first by yourself but still if you are getting trouble then move on to tutorials.

Here we require to maximize the cake volume each person would get:

Constraints:
1.  Each person would get equal volume of cake.
2.  We will not mix two cake pieces to make one piece.





 Now for Example:

 Let's suppose 3 friends are coming up for party and volume of cakes are 26 26 50. Now we want to divide total of 102 volume. So, if we divide larger cake into 4(3 friends and one himself) parts each person would get 50/4=12.5 volume of cake which is not the optimal solution. The optimal solution would to give each one 25 volume cake in this way each one would get maximum volume he can get (25 from first + 25 from second + 2*(25 from third)). 
In this way we will get maximum volume of cake. So, lets try this out in form of code.


Approach:

1. First we will find volume of each cylindrical cake present and store in a arraay.
2. Sort the array and take last element which will the maximum volume of a pie among all pieces present.
3. Apply binary search on 0 to maximum volume (element obtained in previous step).
4. For each mid value obtained from binary search check if that value of mid is going to suffice all his friends.
5. Do this until you find a precise mid value.

Some code snippets are:

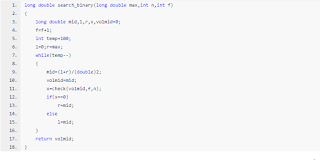
Binary search Code:

Important points:

1. Here we have run while loop for binary search 100 times to maximise precision. In this way we will obtain maximum precise value possible under given constraints.
2. Check function checks if the Mid volume obtained satisfy given conditions and all friends get their share. See below code snippet for check function.
3. max is the maximum volume of all given volumes of pie.
4. f is no. of friends and we have added 1 to it because the person himself also wants cake.

Check function code:

Important points:

1. b[i] here is the array that contains sorted order of volumes of PIE.

2. sum stores number of friends that can be satisfied by this mid-value volume of PIE.

So, Finally return the so obtained value of mid after 100 operations and that is our answer.

I have tried my best to explain solution in best possible manner. Try it and if you are facing any problem you can contact for solution or comment below.